Overview

Ambiguity and uncertainty abound in natural language. In this lesson, we'll learn the basics of probability which will help us to quantify that uncertainty.

Outcomes

After completing this lesson, you'll be able to ...

• estimate the probability of a single event
• estimate the joint probability of two events
• estimate the conditional probability of two events

Background

Probability is a measure of how likely or unlikely something is to happen.

It is a way of quantifying uncertainty about an event by assigning it a value ranging from 0 to 1.

If an outcome is impossible, its probability is 0.

If an outcome is certain, its probability is 1.

The closer a probability is to 1, the more likely it is to happen.

We measure probability by counting and normalizing (dividing by some total) to ensure that we get a value between 0 and 1.

Discrete probability distributions

Probabilities can describe continous and discrete events. Continuous events are those that can take an infinite number of values (ex. formant values for various speech signals, heights of people at various ages, etc.). We'll focus on discrete events here, as it much of what we'll discuss in this course and later ones falls into this category (ex. classification tasks, text generation, etc.).

Discrete events are those with a countable number of possible outcomes. As an example, imagine a six-sided "dice"³ where each side represents one of six possible outcomes of a roll (1,2,3,4,5,6):

However many times we roll the "dice", each result will match one of those six possible outcomes (i.e., we'll never roll a 2.743).

Marginal probabilities

To calculate the probability of rolling a 3 with a fair six-sided "dice", we simply count the number of faces that show a 3 and divide by the total number of faces:

$P(X = 3) = \frac{1}{6}$

More generally, ...

$P(X = x) = \frac{count(\text{outcome of interest})}{count(\text{all possible outcomes})}$

In the example above, $X$ refers to a discrete random variable. As we saw, discrete simply means a countable number of possible values (outcomes). A random variable just means that the sum of probabilities over all possible outcomes (values) of the variable sum to 1 to form a probability distribution.

$P(X = x)$ is known as a marginal (simple) probability.

Distributions

If we didn't know the "dice" was fair, we could figure this out by rolling many many times:

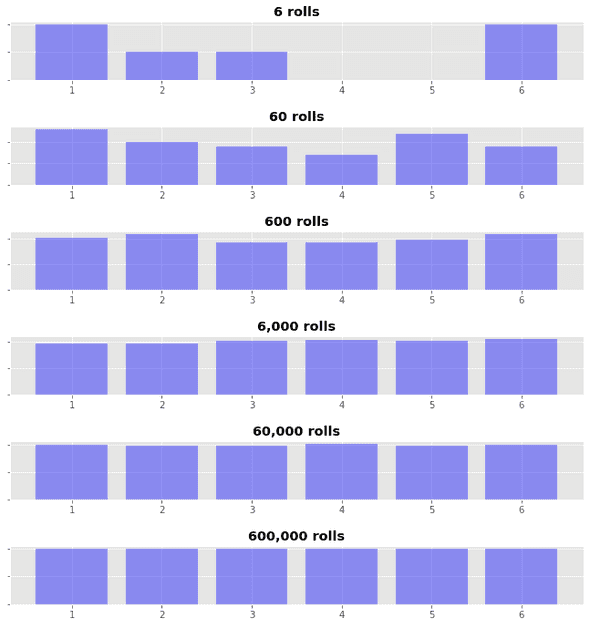
If we could roll the "dice" an infinite number of times, we could calculate the true probability of each possible outcome.

To use terminology from probability theory, each roll is a trial / experiment /event. Each event has a particular outcome.

At the end of a series of trials, we are left with a distribution of possible outcomes. In the case of a fair six-sided "dice", we have a uniform distribution: each outcome is equally likely or equiprobable.

Though it isn't uniform, the frequency of characters and token types also form a distribution:

What kinds of words occur most frequently? What is their grammatical category? Do they form a natural class?

The Zipfian distribution has been demonstrated to hold for many human languages. What does this tell us about the nature of human language?

The probability of A OR B

What about cases where we're interested in the union of two or more possible events $P(A \cup B)$?

If the two events are disjoint (no overlap), then $P(A \cup B)$ is simply $P(A) + P(B)$.

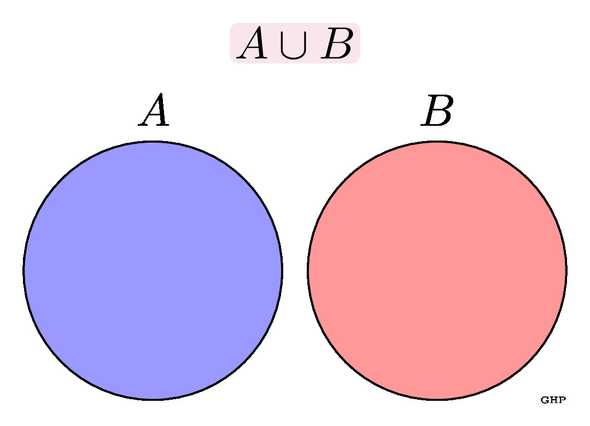
If the two events are mutually exclusive (i.e., they both can't happen at the same time) or disjoint (their intersection is empty), this turns out to just be a matter of addition:

$P(a \vee b) = P(a) + P(b)$

We're not limited to pairs of events.

For example, let's say we want to calculate the probability of rolling an even number. There are three outcomes that satisfy this condition:

$P(\text{even roll}) = P(\texttt{roll}(2) \vee \texttt{roll}(4) \vee \texttt{roll}(6))$

• $P(\texttt{roll}(2)) = \frac{1}{6}$
• $P(\texttt{roll}(4)) = \frac{1}{6}$
• $P(\texttt{roll}(6)) = \frac{1}{6}$

$P(\text{even roll}) = P(\texttt{roll}(2)) + P(\texttt{roll}(4)) + P(\texttt{roll}(6))$

$P(\text{even roll}) = \frac{1}{6} + \frac{1}{6} + \frac{1}{6} = \frac{3}{6} = \frac{1}{2}$

Note that $P(a \vee b)$ will never be smaller than $P(a)$ or $P(b)$.

If the events have some overlap, we need to avoid counting the overlap twice, so we need to subtract $P( A \cap B)$ once:

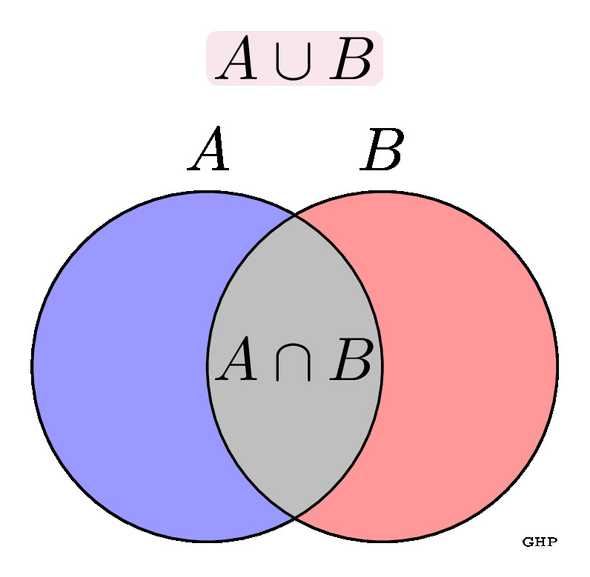
$P(A \cup B) = P(A) + P(B) - P( A \cap B)$ will work in all cases. What will $P( A \cap B)$ be if $A$ and $B$ are disjoint?

The probability of $\neg A$

We've looked at single outcomes and disjunctions of outcomes. What about the probability of some outcome $A$ not happening?

$P(\neg A) = 1 - P(A)$

In other words, in an event with discrete outcomes (ex. rolling a "dice"), the probability of something happening is 1 (i.e., the sum of all possible outcomes²). The chance of a particular outcome not occuring is then the sum of the probability of every other event.

Let's apply this to an example.

For a fair six-sided "dice", what is the probability of not rolling a 6?

$P(\neg\texttt{roll}(6)) = P(\texttt{roll}(1)) + P(\texttt{roll}(2)) + P(\texttt{roll}(3)) + P(\texttt{roll}(4)) + P(\texttt{roll}(5))$

$= 1 - P(\texttt{roll}(6))$

Let's try combining this rule with one we saw previously...

For a fair six-sided "dice", what is the probability of not rolling a 2 or 4 ($P(\neg 2 \vee \neg 4)$)?

$1 - \frac{1}{6} - \frac{1}{6} = \frac{4}{6} = \frac{2}{3}$

Joint probabilities

Joint probability measures the likelihood of two events occurring simultaneously.

The joint probability of event $A$ and event $B$ is commonly represented using one of the following formats:

• $P(A, B)$
• $P(A \land B)$
• $P(A \; \text{and} \; B)$

It's the fraction of outcomes where $A$ and $B$ are both true:

$\frac{\text{count(A and B)}}{\text{count(all outcomes)}}$

Independent events

If two events are independent, that means that the two events do not influence one another.

The joint probability of two independent events is defined as the product of their individual probabilities:

$P(A, B) = P(A) * P(B)$

Let's see why.

For a fair six-sided "dice", what is the probability of rolling a 2 and then rolling a 5?

While we're interested in one particular outcome of two rolls, it's important to remember that each roll is independent: the outcome of one roll does not depend in any way on another.

There are 36 possible outcomes of two rolls:

from itertools import product

# 1, 2, ..., 6
roll_outcomes = range(1,7)
# i.e., $6^{2}$ possible outcomes
print(sum(1 for outcome in product(roll_outcomes, repeat=2)))

Only one of them shows a 2 followed by a 5:

from itertools import product

# 1, 2, ..., 6
roll_outcomes = range(1,7)
# i.e., 6^{2}
for outcome in product(roll_outcomes, repeat=2):
  if outcome == (2, 5):
    print(outcome)

When asking for the probability of such an event, we're simply asking for the portion of outcomes that match our criteria (i.e., 1 out of 36):

$\frac{1}{36}$

To solve this another way, let's use the definition of joint probabilities:

$\frac{1}{6} * \frac{1}{6} = \frac{1}{36}$

Ok, let's try applying this to measure the probability of more than one possible outcomes.

What is the probability of (rolling a 2 and then a 5) OR (rolling a 5 and then a 2)?

We know from the last example that there are 36 possible outcomes for two rolls. We're interested in 2 of those 36 possibilities:

from itertools import product

# 1, 2, ..., 6
roll_outcomes = range(1,7)
# the subset of the $6^{2}$ outcomes that match our criteria
print(
  sum(
    1 for outcome in product(roll_outcomes, repeat=2) \
    if outcome == (2, 5) or outcome == (5, 2)
  )
)

Let's apply our definition of joint probabilities:

$P(\text{rolling a 2 and then a 5}) = \frac{1}{6} * \frac{1}{6} = \frac{1}{36}$

$P(\text{rolling a 5 and then a 2}) = \frac{1}{6} * \frac{1}{6} = \frac{1}{36}$

Now let's combine those (i.e., $P(A \vee B)$):

$P((\text{rolling a 5 and then a 2}) \vee (\text{rolling a 2 and then a 5})) = P(\text{rolling a 2 and then a 5}) + P(\text{rolling a 5 and then a 2})$

$\frac{1}{36} + \frac{1}{36} = \frac{2}{36} = \frac{1}{18}$

Independence

Related to our last example is the idea of independence.

If $P(a, b) = P(a)P(b)$, $a$ and $b$ are completely independent. In other words, if the occurence of one event, $a$, has no effect on the likelihood of another event, $b$, then the two events are independent.

Examples include rolls of a "dice" and coin flips. Now that you know how to caculate marginal and joint probabilities, you can test independence on less obvious cases.

Conditional probabilities

We talked about independent events, but what about cases where one outcome affects another?

$P(A\vert B)$ : What is the probability of $A$ given $B$?

In other words, assuming $B$ has occurred, what is the probability of $A$ then occurring?

$P(A \vert B) = \frac{P(A, B)}{P(B)}$

Note that this is a question about the portion of $B$ outcomes (rather than all outcomes) that coincided with $A$.

For example, if a roll of the "dice" results in a 2, what is the probability that the sum after a second roll will be less than 4?

$P(B = sum < 4 \vert A = 2)$

How do we go about caculating $P(B = sum < 4 \vert A = 2)$? If we're feeling lazy, we could write something like the following:

from itertools import product

# 1, 2, ..., 6
roll_outcomes = range(1,7)
# the subset of the $6^{2}$ outcomes that match our criteria
valid_outcomes = lambda: (outcome for outcome in product(roll_outcomes, repeat=2) \
  # criteria for A
  if outcome[0] == 2 \
  # criteria for B
  and sum(outcome) < 4
)

vo = list(valid_outcomes())
print(f"valid outcomes:\t{vo}")
print(f"num. valid outcomes:\t{len(vo)}")

Of the 36 possible outcomes of two rolls of a six-sided "dice" ($6^{2}$), the only time the sum of two rolls will be less than 4 when the first roll is 2 is the ordered pair (2, 1). $P(B = sum < 4 \land A = 2)$ is thus $\frac{1}{36}$.

We also know $P(A = 2) = \frac{1}{6}$.

That's all we need to determine $P(B = sum < 4 \vert A = 2)$:

$P(B = sum < 4 \vert A = 2) = \frac{\frac{1}{36}}{\frac{1}{6}} = \frac{1}{36}\frac{6}{1} = \frac{1}{6}$

This hopefully makes intuitive sense. There are only six possible options for the second roll. Only one of those six meets our criteria ($B = sum < 4$). We shouldn't treat this as a case out of 36, because the outcome of the first roll has constrained the space of outcomes we need to consider.

What if we wanted to calculate $P(B = sum \geq 4 \vert A = 2)$?

from itertools import product

# 1, 2, ..., 6
roll_outcomes = range(1,7)
# the subset of the 6^{2} outcomes that match our criteria
valid_outcomes = lambda: (outcome for outcome in product(roll_outcomes, repeat=2) \
  # criteria for A
  if outcome[0] == 2 \
  # criteria for B
  and sum(outcome) >= 4
)

vo = list(valid_outcomes())
print(f"valid outcomes:\t{vo}")
print(f"num. valid outcomes:\t{len(vo)}")

$\frac{\frac{5}{36}}{\frac{1}{6}} = \frac{5}{36} \frac{6}{1} = \frac{5}{6}$

Another way of saying $P(B = sum \geq 4 \vert A = 2)$ is $P(B = \neg (sum < 4) \vert A = 2)$. Using this reformulation, we can apply our rule for $P(\neg A)$ here:

$P(\neg A) = 1 - P(A)$

$1 - P(B = sum < 4 \vert A = 2) = 1 - \frac{1}{6} = \frac{5}{6}$

We get the same answer. Coincidence? Unlikely! :)

There a few other terms that can help us to make sense of conditional probabilities. In the context of $P(A \vert B)$ , $P(A)$ represents the likelihood before we receive some important new information. For this reason, it's referred to as the prior (prior = before). In the same vein, $P(A \vert B)$ is known as the posterior as it represents our updated estimate of the likelihood after incorporating some important new information.

Next steps

You now know the basics of estimating probabilities. In the next lesson, we'll apply this information to estimate the probability of sequences. Before moving on, though, let's practice ...

Practice

• Using a single fair "dice", you've rolled 6 three times in a row. What is the probability of rolling a 6 on the next roll?

• Using a fair "dice", what is the probability of rolling a 3 four times in a row?

• Using a fair "dice", what is the probability of not rolling a 3 within six rolls?

• Is $P(a \vee b)$ ever smaller than $P(a)$? Why or why not?

• Determine whether the following describe dependent or independent events:

  • Drawing cards from a standard deck of 52 cards without replacement
  • Drawing cards from a standard deck of 52 cards with replacement
  • Rolling a "dice" repeatedly
  • The order of words

• Give an example of a pair of words with strong or weak dependence

• Give an example of a sequence of words that would have a probability of 0.

Related resources

• https://en.wikipedia.org/wiki/Gambler%27s_fallacy

• https://www.khanacademy.org/math/statistics-probability/probability-library